
Bertha Medina Flores
Dulce Ma. Peralta G. R.
Beatriz Ojeda Salcedo
En este trabajo se retoma la labor hecha durante más de 25 años en el CCH en la búsqueda de alternativas para elevar el aprovechamiento académico de nuestros alumnos. Las experiencias que nos han permitido arribar a la metodología de enseñanza actual incluyen la investigación educativa y la experimentación.
Este trabajo consta de dos partes, la primera se refiere a la importancia del desarrollo de las habilidades cognitivas básicas e incluye la orientación pedagógica para promoverlas en los estudiantes y, la segunda, describe en detalle, con dos ejemplos, cómo se llevan a cabo las estrategias y actividades didácticas que consideramos ayudan a la consecución de dichas habilidades.
Presentamos aquí, algunas formas de hacer matemáticas en el aula. Las estrategias y actividades están diseñadas para proporcionar al alumno variados contextos cotidianos y científicos que sirven de pretexto para abordar los contenidos matemáticos del plan de estudios y promover las habilidades básicas que todo bachiller debe desarrollar, es decir, saber representar, calcular, usar la tecnología, leer, escribir y hablar con matemáticas.
En el ámbito del conocimiento, las matemáticas nos proporcionan recursos de lo más poderoso que existe para modelar y resolver problemas. Estos recursos matemáticos abarcan un amplia gama de temas, tanto en las ciencias exactas y naturales, como en las disciplinas sociales y las humanidades, sin olvidar la tecnología.
Química, física y biología son ejemplos clásicos de disciplinas del conocimiento que usan técnicas y métodos matemáticos para modelar situaciones y resolver problemas. Muchas de las técnicas y métodos matemáticos que aplican son valiosos por su cualidad de generalización, pero justamente este potencial de generalización es ahora cuestionado por investigadores de la cultura y la cognición1 y algunos docentes de las ciencias, distintas a las matemáticas, han empezado a compartir parte de estas críticas. Mientras abundan los trabajos que estudian como se usan las matemáticas en la práctica cotidiana, escasean los trabajos que tomen una perspectiva similar con respecto a las prácticas escolares tales como la ciencia2. Independientemente de lo que se cuestione, lo cierto es que muchos alumnos, a pesar de haber cursado matemáticas y de estar cursándolas en el momento en que estudian otras materias —científicas o no— son incapaces de aplicar los métodos matemáticos en ellas.
Estamos en la orientación, como en otros países, de continuar investigando nuestra práctica docente cotidiana para afinar propuestas con relación a una nueva concepción de la educación en la ciencia que resalte las aptitudes y habilidades que los alumnos requieren para tener éxito en los cursos científicos.
Las HAB pueden ser definidas como aquellas destrezas y capacidades intelectuales amplias, esenciales para el trabajo efectivo en todos los campos de estudios académicos. Ellas proporcionan el vínculo que articula entre sí a las áreas del conocimiento aunque no son específicas a ninguna disciplina en particular. Las HAB son: la lectura, la escritura, la capacidad para expresarse, la capacidad para escuchar, las matemáticas entendidas como lenguaje, la capacidad de razonar y estudiar y el desarrollo de una cultura de cómputo.
La sociedad hoy en día exige que la escuela proporcione a sus estudiantes una cultura matemática que les permita ser ciudadanos bien informados, capaces de entender las cuestiones propias de una sociedad tecnológica; por lo que se hace necesario hacer un cambio en los enfoques y contenidos matemáticos así como en las metodologías de enseñanza tradicionales. Las nuevas metodologías deben contemplar la experimentación, el uso de las tecnologías y comunicación de las ideas matemáticas, así como el razonamiento matemático entendido como la representación de las ideas en forma de poderlas comunicar.
En el documento del Consejo Nacional de Profesores de Matemáticas de los Estados Unidos se proponen cinco metas principales para los niveles de Preprimaria hasta el último año de la enseñanza media superior que son importantes considerar ya que también han sido ejes conductores en la revisión de los programas de matemáticas en nuestro país. El logro de estas metas supone que el alumno debe:
- Ser capaz de resolver problemas matemáticos
- Aprender a comunicarse matemáticamente
- Aprender a razonar matemáticamente
- Saber valorar las matemáticas
- Tener confianza en su capacidad de hacer matemáticas
Estos objetivos implican que los estudiantes experimenten situaciones abundantes y variadas, relacionadas entre sí, que los lleven a valorar las tareas matemáticas, desarrollar hábitos mentales y entender y apreciar el papel que las matemáticas cumplen en los asuntos humanos; que debe animárseles a explorar, predecir e incluso cometer errores y corregirlos de manera que adquieran confianza en su propia capacidad de resolver problemas, que deben leer, escribir y debatir sobre las matemáticas, y deben formular hipótesis, comprobarlas y elaborar argumentos sobre su validez. Si el alumno desarrolla estas capacidades, seguramente estará adquiriendo potencial matemático.
Aprender a valorar las matemáticas: Apreciar el papel que cumplen las matemáticas en el desarrollo de nuestra sociedad actual y explorar las relaciones que existen entre la matemática y las disciplinas a las que sirve.
Adquirir seguridad en la propia capacidad: Las matemáticas en la escuela deben hacer que todos los estudiantes comprendan que usar la matemática es una actividad humana corriente.
Ser capaz de resolver problemas matemáticos: Desarrollar esta capacidad es esencial si se quiere que los estudiantes sean ciudadanos productivos. Algunos de estos problemas deben ser abiertos, sin solución única y otros deben ser formulados por el propio estudiante.
Aprender a comunicarse matemáticamente: El desarrollo de esta competencia implica por parte del estudiante el aprendizaje de los signos, símbolos y terminología de las matemáticas. Esto se consigue mejor en situaciones de problema donde los alumnos tienen la oportunidad de leer, escribir y discutir sus ideas para las que el uso del lenguaje matemático es algo natural.
Aprender a razonar matemáticamente: Para trabajar con las matemáticas es fundamental formular hipótesis, recopilar evidencias, hacer pronósticos y elaborar argumentos que apoyen estas nociones.
Uso de la tecnología: En contra de los miedos de muchos, la disponibilidad de calculadoras y computadoras ha ampliado la capacidad de cálculo para los estudiantes, éstos han de ser capaces de decidir cuándo tienen que efectuar un cálculo o si necesitan una respuesta exacta o aproximada. Deben ser capaces de elegir y usar la herramienta más apropiada.
Para atender el desarrollo de estas HAB nos hemos dado a la tarea de elaborar actividades y materiales didácticos adecuados y hemos diseñado las estrategias de aplicación en el aula para provocar que los aprendizajes pretendidos se den efectivamente en nuestros estudiantes. Presentamos aquí, una práctica docente que proporciona a los estudiantes contextos variados así como maneras diversas de hacer matemáticas con los contenidos de las actividades propuestas. El foco siempre es matemáticas y el pretexto puede ser la economía laboral, el crecimiento celular, las mezclas químicas, los negocios en el parque de diversiones, el trabajo infantil, la geometría de la dentadura humana plasmada en una ecuación, el balón de football y el efecto de la gravedad, la carrera con obstáculos, la extinción de las especies, los viajes de Gulliver, cuentos (la hipotenusa del elefante), novelas (el matemático del rey) , juegos (brincando de cojito) películas (Donald en el país de las matemáticas, Apolo 13, Querida encogí a los niños y otras), lecturas y artículos de divulgación científica, artículos de periódico —La banca que tenemos (Fobaproa), Hood Robin (el robo legal), entre otros—, además de obras de teatro (Einstein, Galileo), museos, exposiciones de arte, etc. Pasemos a ver los ejemplos.
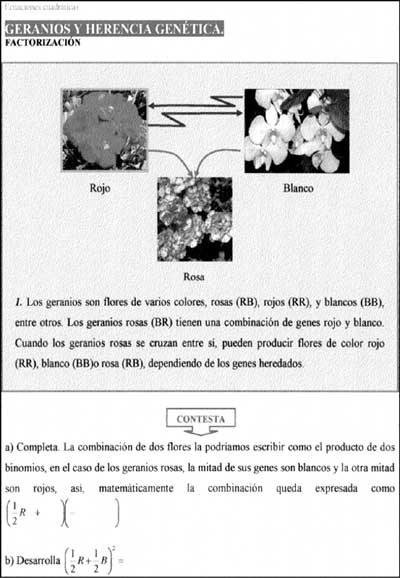
GERANIOS: Conexiones con: la biología, la genética, la probabilidad y el álgebra que modela su reproducción. Esta actividad es llevada a cabo individualmente para después ser comparada con las respuestas de sus pares.






Como consecuencia de aplicar, entre otras, esta actividad en el aula, obtuvimos con menos esfuerzo en la enseñanza, una mayor comprensión del producto de binomios y observamos que la asimilación del concepto de factorización de trinomios y sus algoritmos se cubrieron, incluida la evaluación, en tres semanas contrastadas con las 5 o hasta 6 semanas que anteriormente les llevaba a los estudiantes comprenderla al 70%, porque ni siquiera aspiraban al 80 de calificación. Para terminar, sólo nos resta decir que existen otras actividades, entre ellas hay prácticas experimentales, que nos han permitido mostrar las matemáticas con más sentido y que hacen de su aprendizaje algo nuevo para los estudiantes y de su enseñanza una actividad motivadora para nosotras las maestras. Nos habría gustado agregar otros ejemplos, pero por desgracia, el espacio aquí no alcanza.
Bibliografía
Campos, M. A., Corona, L. «Universidad y vinculación: nuevos retos y viejos problemas» IMASS-UNAM. México, 1994.
College Entrance Examination Board. Academic Preparation in Science. Teaching for Transition from High School to College. New York, 1990.
Jiménez Gómez, E.; Solano Martínez, I.; Marín Martínez, N. «Problemas de terminología en estudios realizados acerca de «lo que el alumno sabe» sobre ciencias», en Enseñanza de la Ciencias, Vol. 12, Num. 2, pp 235-245, 1994.
Kent, D. «Algunos procesos a través de los cuales se pierden las matemáticas». Educational Research, Vol 21, Num 1. 1986.
Knill, G. et al. Mathpower 10. McGraw-Hill. Ontario, Canadá. 2000.
Malerba, Luigi. La hipotenusa del elefante. Austral Juvenil, ESPASA CALPE, Madrid, 1987.
Postic, Marcel. «El análisis de las dificultades de los alumnos a la transformación de las prácticas educativas» El aula Universitaria, Aproximaciones Metodológicas Cise-UNAM 1991. Comp.
Rugarcía, A. «El método para enseñar». Panorama Educativo, julio- diciembre 1992, pp. 34-40
Varela, G. «La cultura política de las universidades de cara al siglo veintiuno». En revista: Universidad Nacional de México. No. 520, 1994, pp. 19-21.
Wenzelburger, E., Scoot, P. «Currículum y evaluación de estándares para la escuela de matemáticas». Reseñas. En revista: Educación Matemática, vol. 1, No.3, México, Iberoamericana, 1989.
Notas
1. Lave, J. 1988. Cognition in Practice, Cambridge University Press. Cambridge, U. K Rogoff, B. and Lave, J. 1984. Everyday Cognition: Its Development in Social Context. Harvard University Press, USA.
2. Nunes, T., Schliemann, A. And Carraher, D. 1993. Street Mathematics and School Mathematics. Cambridge University Press, Cambridge, U. K.
Articulo publicado en la Revista Xictli de la Unidad UPN 094 D.F. Centro, México. Se permite su uso citando la fuente. Dirección u094.upnvirtual.edu.mx