La numeración posicional y el cero mesoamericano. Knorosov y la escritura maya

Arturo Corzo Gamboa
Asesor de la Unidad UPN 094

El pueblo maya logró desarrollar una excepcional cultura matemática y astronómica de la cual es un ejemplo sobresaliente el calendario o haab, que era más exacto que el de los europeos cuando llegaron a América, pues los mayas habían logrado establecer la duración del año en 365.2420 días (en la actualidad se ha fijado en 365.2422 días), mientras que el de los europeos había ya acumulado varios días de retraso. Tan considerable era éste, que el Papa Gregorio XIII, para corregir esa imprecisión que venía arrastrando el calendario juliano, ordenó, en 1582, que se eliminaran doce días; ese año no existieron los días del 4 al 15 de octubre. Noventa años antes, Colón había llegado a las Antillas, y bien sabemos que lo hizo un 12 de octubre que, en la cuenta correcta, correspondería a una fecha posterior. (Las fechas históricas ya no se pueden cambiar; pero siempre será benéfico saber lo que ha ocurrido). Otro ejemplo singular del pensamiento maya lo constituye el sistema de numeración posicional, con el cero como cantidad matemática, el cual fue «conocido y utilizado por los pueblos de la costa del golfo («olmecas») y [por] los constructores de Monte Albán I (¿zapotecas?) varios siglos antes que los mayas lo emplearan».(1) Es decir, el uso de una numeración posicional que incluía el cero, se dio primero entre los olmecas –la «cultura madre»– y, posiblemente, entre los zapotecas, para luego alcanzar un gran desarrollo entre los mayas.

La creación del cero en Mesoamérica es una primicia mundial; ya que, hasta donde se sabe, ningún otro pueblo lo concibió antes. Esto es muy importante porque siempre se dio por cierto que la numeración posicional y el cero se habían desarrollado una sola vez en la historia de la humanidad: en la India, donde en el siglo VIII de nuestra era empezó a usarse el sistema decimal. Los árabes llevaron esa numeración hasta España, país del que se empezaron a adueñar en 712, y desde ahí la difundieron por el resto de Europa. (Por eso se dice, erróneamente, numeración arábiga, sin ser los árabes sus creadores; lo más correcto sería llamarla numeración hindú). Una agradable coincidencia es que los dos pueblos indios de la historia, el maya (por la equivocación de Colón) y el hindú, fueron los inventores de esa proeza del pensamiento abstracto que es el cero. Proeza intelectual comparable a la que llevaron al cabo los griegos Demócrito y Leucipo, en el siglo V a.C., al elaborar su teoría atomística con la única herramienta que podían utilizar: el pensamiento.

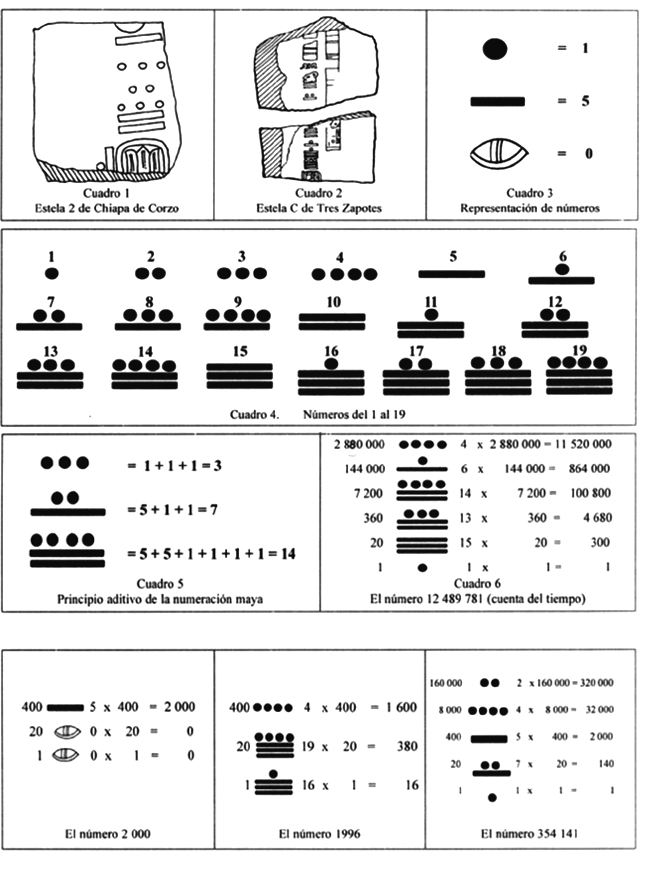
El cero de los mayas aparece en la Estela 2 de Chiapa de Corzo, estado de Chiapas (véase el cuadro 1), en un numeral que corresponde al año 35 a.C., y también en la Estela C de Tres Zapotes, estado de Veracruz (cuadro 2), en otro numeral correspondiente al año 31 a.C. (2) El mayista Sylvanus G. Morley afirmó que los sacerdotes habían ideado ese sistema de numeración cuyos valores dependen de la posición que los símbolos numéricos guardan entre sí, en una época que puede ubicarse dentro de los siglos IV ó III a.C. (3) y, por supuesto, mucho antes de que el sistema de posiciones en la numeración fuera de uso general en la Europa occidental.

Los símbolos que los mayas utilizaron para representar los números fueron solamente tres: el punto, para el 1; la línea horizontal, para el 5; y el dibujo de una concha, para el cero. (Véase el cuadro 3).

Con la combinación de estos tres símbolos escribieron todos los demás números. En el cuadro 4 aparecen los números del 1 al 19.

El principio aritmético que utilizaron los mayas fue el aditivo, como se muestra en el cuadro 5.

Los numerales eran colocados verticalmente y se leían de arriba hacia abajo. El valor de los rangos, tomando en cuenta que el sistema era vigesimal, es como a continuación se muestra (4):

6° rango = 3’200,000 (160,000 x 20)

5° rango = 160,000 (8,000 x 20)

4° rango = 8,000 (400 x 20)

3er. rango = 400 (20 x 20)

2° rango = 20 (1 x 20)

1er. rango = 1 (1 x 1)

El rango que sigue a 3’200,000 es 64’000,000 y así, sucesivamente.

Para el cómputo del tiempo los sabios mayas modificaron el tercer rango, pues no emplearon la segunda potencia de 20, (400), sino 360, que es el producto de 18 x 20. Esto se debió a que 18 era el número de meses de 20 días cada uno en el calendario. Para el valor de los demás rangos se utilizó de nuevo el 20 como factor, tal como aparece en el cuadro siguiente:

6° rango = 2’880,000 (144,000 x 20)

5° rango = 144,000 (7,200 x 20)

4° rango = 7,200 (360 x 20)

3er. rango = 360 (20 x 18)

2° rango = 20 (1 x 20)

1er. rango = 1 (1 x 1)

Utilizando los valores anteriores, el número 12’489,781 en la cuenta del tiempo de los mayas (el cual aparece en la página 61 del Códice de Dresde), se escribe como se muestra en el cuadro 6.

En Quiriguá, Guatemala, fue encontrada una estela que muestra un texto en el que hay una cantidad que se remonta hasta 400 millones de años, lo que confirma la profundidad del pensamiento matemático y astronómico de aquel pueblo admirable.

Esta sencilla exposición sobre la capacidad creadora de los mayas no estaría completa si no agregáramos un comentario de los trabajos que se han hecho para descifrar su escritura. Durante casi cinco siglos esa escritura fue un enigma, y se llegó a creer que jamás se encontraría la clave para leerla. No se veía en el horizonte a ningún mayista que pudiera hacer con los glifos mayas la hazaña que Champollion realizó con los jeroglíficos egipcios. Y no se veía quizá porque estaba muy lejos, allá en la entonces Unión Soviética, donde trabajaba arduamente el lingüista ucraniano Yuri Valentinovich Knorosov. Este insigne mayista había empezado a interesarse en la escritura de los mayas justamente en 1945, a finales de la Segunda Guerra Mundial, cuando el ejército ruso se apoderó de Berlín. Knorosov tenía entonces 21 años de edad y era soldado del Ejército Rojo. «Participaba de la toma de Berlín cuando descubrió que [los soldados] estaban vaciando la gran Biblioteca Nacional de la capital alemana y que los libros eran empacados en cajas para su traslado. Al acercarse encontró los ejemplares de [fray Diego de] Landa [Relación de las cosas de Yucatán] y [una reproducción de los códices mayas hecha por] los [hermanos guatemaltecos Antonio y Carlos] Villacorta, y comenzó su lucha por hacer factible lo imposible» (5). Ése fue el preciado botín de guerra que le tocó a Knorosov: iban en su alforja las semillas del pensamiento maya y él estaba destinado a ser el descubridor del engranaje de su expresión escrita.

Años después, en el Instituto Etnográfico de Leningrado (hoy San Petersburgo), y con el gran inconveniente de no poder viajar a México o a Centroamérica, se dedicó a buscar la clave para el desciframiento de los glifos mayas. Sus estudios encontraron la recia oposición del británico Eric J. Thompson, considerado en esos años la máxima autoridad en estudios mayas, quien rechazó todo lo que Knorosov propuso, por el solo hecho de «considerarlo comunista». (6) Sin embargo, algunos investigadores de Harvard siguieron las pistas que Knorosov había descubierto; aunque modificando algunos conceptos esenciales. Knorosov no estuvo de acuerdo con ellos y, en una visita que hizo a México (1995) dijo «que no podía estar de acuerdo ‘ni por cortesía’ con las interpretaciones de los estadounidenses, porque la escritura maya, ‘como cualquier otra escritura del mundo tiene sus reglas lingüísticas severas y el problema es que ellos han sido poco rigurosos. Han interpretado los signos por separado en lugar de hacer lecturas de textos mayas absolutamente comprensibles.’»(7). En 1991 viajó por primera vez a Guatemala, donde el gobierno de ese país le otorgó la Orden del Quetzal. En 1994 el gobierno mexicano le entregó la Orden del Águila Azteca, la que recibió en la embajada de México en Moscú. (8) Un gran mayista, como lo es Michael D. Coe, cuenta que Thompson le confió un poco antes de morir: «Yo ya no veré los resultados de las investigaciones que se están haciendo sobre la escritura de los mayas; pero usted vivirá aún y se dará cuenta de quién tuvo la razón: ese maldito ruso o yo». Hoy todos sabemos que ganó «ese bendito ruso».

Decía Knorosov: «Lo creado por una mente humana puede ser resuelto por otra mente humana»; es decir, Knorosov jamás creyó en la imposibilidad del desciframiento, y luchó contra la dificultad natural del enigma y contra los obstáculos que deslealmente le pusieron enfrente Thompson y su grupo. Hay una frase del gran poeta norteamericano Edgar Allan Poe que puede aplicarse a la firme convicción del sabio Knorosov: «Pocas personas pueden creer que es difícil inventar un método de escritura secreta que desafíe la investigación. Sin embargo, puedo asegurar que el ingenio humano no puede crear un cifrado que el ingenio humano no pueda descifrar» (9).

Desafortunadamente, nadie se interesó en México por publicar los resultados de su trabajo, aunque tuvo aún la satisfacción en sus últimos días de saber que el grupo Xcaret y la Universidad de Quintana Roo editarían su grandiosa obra. Knorosov estuvo al tanto vía correo electrónico de los avances del primer tomo de los dos que se programaron. El ejemplo del investigador ruso es aleccionador: «A miles de kilómetros de distancia aprendió español y trabajó en silencio con la compañía que pueden brindar un gato, un cigarrillo y una botella de vodka. Si bien sus aportaciones son ‘insuperables’, Knorosov murió solo –a causa de un derrame cerebral y una neumonía que contrajo al permanecer varios días en [el] pasillo helado [de un hospital]– y fue enterrado en un antiguo basurero de San Petersburgo [antes Leningrado]» (10).

Para las naciones que hoy están asentadas en el área cultural que Kirchhoff llamó Mesoamérica, es un orgullo conmemorar el grandioso pasado del pueblo maya y de las culturas que le sirvieron de soporte. Saber que los mayas fueron capaces de desarrollar un sistema de numeración con el cero como invención básica, y que escribieron en las estelas pétreas su historia, su cosmogonía y los aconteceres de su vida cotidiana, debe servir para recuperar la confianza en la capacidad intelectual de nuestros pueblos.

Notas:

1 Alberto Ruz Lhuillier, La civilización de los antiguos mayas, La Habana, Editorial de Ciencias Sociales, 1974, p. 89.

2 Juan Tonda y Francisco Noreña, Los señores del cero. El conocimiento matemático en Mesoamérica, México, Consejo Nacional para la Cultura y las Artes/PanGea Editores, 1991, pp. 27-29.

3 Sylvanus G. Morley, La civilización maya, México, Fondo de Cultura Económica, 1972, p. 252.

4 Tonda y Noreña, op. cit., p. 22.

5 Miryam Audiffred, «Lo creado por una mente humana puede ser resuelto por otra, decía Knorosov», en La Jornada de enmedio, viernes 16 de junio de 2000, p. 8 a.

6 Adriana Malvido, «Murió Knorosov, artífice de la clave para descifrar glifos mayas», en La Jornada, jueves 1 de abril de 1999, p. 3.

7 Ibidem.

8 Ibidem.

9 Edgar Allan Poe, cit. en José Antonio de la Peña, Álgebra en todas partes, México, Secretaría de Educación Pública/Fondo de Cultura Económica/Consejo Nacional de Ciencia y Tecnología, (Col. «La ciencia para todos», 166), 1999, p. 87.

10 Audiffred, op. cit.