Bertha Medina Flores y Dulce Ma.
Peralta González Rubio
CCH Sur
Beatriz Ojeda Salcedo
UPN
Además de un símbolo que lo representa (numeral), cada número tiene nombre. Cuando empezamos a aprender a contar, lo hacemos siempre en voz alta, repetimos la serie de nombres para cada numeral que otros pronuncian para nosotros. Recitamos los números para memorizarlos, y no sólo eso, cuando hacemos cálculos, no los pronunciamos en voz alta -como cuando pequeños- pero nuestros cerebros los “subvocalizan”(1) para “guardarlos ahí” —en el pizarrón mental—. Necesitamos “oírlos” otra vez en nuestras mentes mientras encadenamos las operaciones con los resultados, si no lo hacemos, los olvidamos —¡Ay, para qué me hablaste!, ¡estoy sumando y ya se me olvidó cuánto llevaba!— es una expresión muy común para todos nosotros. Es por ello que casi toda clase de ruidos o sonidos interfieren con nuestra capacidad de cálculo. Hacer operaciones aritméticas requiere de tanta o mayor concentración que la lectura.
Devlin, en su libro The Math Gene, narra que en una de sus presentaciones para mostrar sus asombrosas habilidades en cálculos aritméticos de alta complejidad, el matemático Arthur Benjamín corrió a desconectar el sistema de aire acondicionado y aclaró que necesitaba “subvocalizar” los números para retenerlos en su mente, de lo contrario los olvidaba y el ruido interfería con su memoria auditiva. Coincidimos con la conclusión de Devlin, pues parece ser que las personas con habilidades de cálculo aritmético extraordinarias utilizan con mucha eficiencia y alta eficacia sus patrones lingüísticos, en este caso, los “sonidos de los números” —nombres— son reproducidos en sus mentes (2).
Aunque muy pocos de nosotros podemos calcular mentalmente la potencia al cubo de un número con cinco dígitos, todos hemos usado nuestra habilidad humana para recordar los patrones verbales de las tablas de sumar y multiplicar, vamos, ¡si hasta las cantábamos!, “dos y dos son cuatro, cuatro y dos son seis, seis y dos son ocho y ocho dieciséis, brinca la tablita yo ya la brinqué… etc”. Aprendemos recitando las tablas muchas, muchas veces y a no pocos adultos les sucede todavía, años después de haberlas aprendido, que para obtener el producto de cualquier número de dos dígitos repiten mentalmente parte de la tabla. Recordamos el sonido de los nombres de los números, no los números en sí mismos. De verdad, revisemos en nuestro interior y veremos que el patrón que “oímos en nuestra mente” es el mismo que aprendimos cuando teníamos siete u ocho años.
A pesar de las horas de práctica, muchas personas tienen gran dificultad con las tablas de multiplicar. Adultos con inteligencia promedio cometen errores por descuido el 10% de las veces que multiplican. Calcular ciertas multiplicaciones en particular, como por ejemplo 8 X 7 o 9 X 7, puede tomar dos segundos y el 25% de las veces habrá error (las respuestas 8 X 7 = 54 y 9 X 7 = 64). ¿Son correctas? Es bueno averiguar por cuenta propia.
¿Por qué se presenta esta dificultad? Haciendo a un lado las tablas del 1 y del diez que son más fáciles, hay sesenta y cuatro productos (entradas) en el conjunto de las tablas de multiplicar que nos exigen aprender en la escuela primaria; a saber, las que resultan de multiplicar cada uno de los números 2, 3, 4, 5, 6, 7, 8, y 9 por cada uno de los mismos números 2, 3, 4, 5, 6, 7, 8, y 9. La mayoría tienen facilidad con las tablas del dos y del cinco, así que las podemos quitar del conjunto de productos que debemos memorizar y nos quedan 36 entradas. Si a esto aunamos que, quien aprende puede aplicar la conmutatividad para la multiplicación, es decir, 2 X 3 y 3 X 2 “dan lo mismo”, entonces el esfuerzo para los productos “duros de aprender” se reduce a poco más de la mitad, así que: ¡Tan sólo hay que aprenderse veintiún multiplicaciones claves de un dígito por un dígito para dominar las tablas!
Para dar una idea en perspectiva de lo que significa aprenderse estos veintiún productos, pensemos que alrededor de los 7 u 8 años, cuando empezamos a practicar las tablas de multiplicar hay un montón de palabras, nombres, hechos, títulos de películas, juegos y cosas que sabemos y aprendemos con esfuerzo, es verdad, pero sin dificultad. Ciertamente que no recitamos las palabras y sus significados una y otra vez como lo hacemos con las tablas de multiplicar lo que, en resumen, significa que nada malo hay con nuestra memoria, excepto cuando le pedimos que recuerde las veintiún multiplicaciones claves. ¿Por qué?
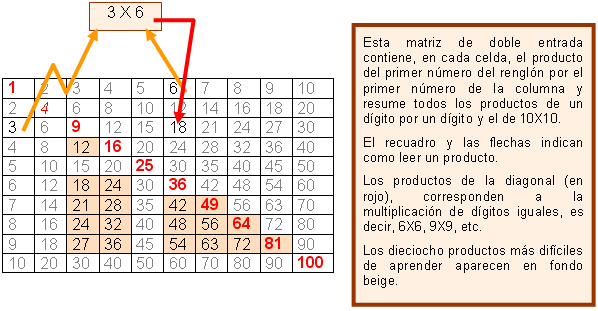
La siguiente tabla es una matriz de doble entrada en cuyas celdas está el producto del número en el renglón por el número en la columna.

Como 3X3, 4X4 y 6X6, son también fáciles, los podemos quitar de la tabla y quedarnos con 18 productos que resultan ser los «duros de aprender» La mayoría de los propios jóvenes comparte la concepción autocrítica de que esta incapacidad para dominar las tablas de multiplicar se debe a su «flojera»; sin embargo, la experiencia personal como docentes nos ha mostrado que no es pereza lo que impide aprender las tablas de multiplicar, sino que hay que buscar qué es lo que hay en las propias tablas que las convierte en «casi imposibles de aprender».
El problema de las tablas de multiplicar no es privativo de México, pues es más general de lo que pensamos; también sucede en otras partes del mundo. Es claro que existe alguna característica en el funcionamiento de nuestro cerebro humano que debemos investigar en vez de juzgar. Hay algo muy significativo que debemos aprender de esto y no son precisamente nuestras tablas de multiplicar. Revisemos nuestra evolución biológica para tratar de explicarnos qué es lo que nos sucede cuando aprendemos las tablas de multiplicar.
Nuestra mente evolucionó como un órgano reconocedor de patrones. La memoria humana trabaja por asociaciones, un pensamiento conduce a otro, “alguien mencionó al tío Genaro y eso nos trajo a la mente la vez que nos llevó al zoológico, donde vimos a una mujer que se parecía mucho a la tía Yolanda, quien se fue a vivir a Baja California, es un lugar donde puedes ir de pesca, cosa que me recuerda al pez vela que…”, y así le seguimos sucesivamente, hilando recuerdos e ideas. Nuestra habilidad para relacionar objetos, ver patrones y reconocer semejanzas es una de las grandes fortalezas de la mente humana.
Las computadoras son extensiones de nuestro cerebro, fueron inventadas para realizar las tareas mentales que llevamos a cabo con penosa dificultad cuando se trata de hacerlas muchísimas veces y de forma rutinaria. Hasta la fecha, una computadora y un cerebro humano son bastante diferentes en sus formas de trabajar. Las computadoras pueden ejecutar billones de operaciones aritméticas en un segundo sin equivocarse, retener grandes cantidades de información sin olvidarla y recuperar dicha información con precisión y bastante facilidad, pero a pesar de las grandes inversiones en talento, tiempo y dinero para construir computadoras capaces de reconocer rostros o que capten el sentido visual de una escena, es algo que aún no se ha logrado en el nivel de eficiencia con el que las ejecutamos los humanos. En comparación con las computadoras, los humanos reconocemos rostros e imágenes panorámicas con facilidad, ya que nuestra memoria funciona a través de asociación de patrones; pero precisamente por esta capacidad no podemos ser tan eficientes con las mismas tareas que las computadoras realizan con facilidad, esto incluye el recordar las tablas de multiplicar y hacer muchos cálculos aritméticos rápidamente sin equivocarnos.
Una fuente del problema en la recuperación memorística de las tablas es que las recordamos lingüísticamente y los resultados de muchas de las entradas se interfieren unos con otros debido a su extremo parecido fonético y simbólico. Una computadora distingue fácilmente —porque así está programada— las diferencias entre 7 X 8 = 56, 6 X 9 = 54 y 8 X 8 = 64, pero nuestra mente ve semejanzas entre estas tres multiplicaciones; en particular, similitudes lingüísticas en la rima que forman las palabras al pronunciar las operaciones, ya sea mentalmente (subvocalizar) o en voz alta (vocalizar). Nuestra dificultad en el intento de mantener estas expresiones separadas es un indicio de las debilidades de nuestra memoria, pero al mismo tiempo, indica una de las grandes fortalezas de nuestra inteligencia. También existen similitudes simbólicas que interfieren con nuestra experiencia y memoria visual, por ejemplo, frente a la expresión 7 X 8 se activan en nuestras mentes varios patrones semejantes entre los cuales se destacan el 48, 56, 54, 45 y 64:
Veamos un equivalente en el entrenamiento lingüístico para mejorar la dicción, trate de reproducir rápidamente el siguiente trabalenguas:
Tres tristes tigres tragaban trigo en un trigal, tigre tras tigre, tigre tras tigre, el trigal se tragaban.
Difícil ¿verdad? Incluso hay dificultad digital al escribirlo, las sílabas tri de trigal y ti de tigre se interfieren entre sí, no importa si se escribe con la mano y un lápiz o con el teclado de la computadora. Son muchas semejanzas, el parecido de la escritura de las palabras y sus correspondientes pronunciaciones se interfieren unas con otras en nuestra mente y rebasan nuestra capacidad de rememoración inmediata, la verdad es que resulta necesario, para la mayoría de las personas, practicarlo para recitarlo correctamente. Este trabalenguas es un clásico ejercicio de entrenamiento para actores y locutores y ¡se parece tanto al de las tablas de multiplicar!
Este fenómeno lingüístico no es privativo de quienes hablamos español. Para el caso de los de habla inglesa, Dehaene explica esto mismo en su libro The number sense (el sentido numérico) con el siguiente ejemplo:
“Suponga que usted tiene que recordar los siguientes nombres y direcciones:
1. Charlie David lives on Albert Bruno Avenue.
2. Charlie George lives on Bruno Albert Avenue.
3. George Ernie lives on Charlie Ernie Avenue.Recordar estos tres hechos parece un reto peculiar. Hay demasiadas semejanzas, lo que produce que cada una de las entradas interfiera con las otras, pero estas son justo las entradas de las tablas de multiplicar. Asigne los dígitos 1, 2, 3, 4, 5, 6 y 7 a los nombres Albert, Bruno, Charlie, David, Ernie, Fred and George respectivamente y sustituya la frase “lives on” por el signo igual y obtendrá las tres multiplicaciones:
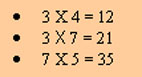 |
Este es el patrón de interferencia que causa los problemas”(3). |
Contra lo que se pudiera creer, es frecuente experimentar que la suma y la multiplicación se interfieran la una con la otra en nuestras mentes, es más fácil y rápido visualizar que 3 X 2 = 7 es incorrecta, que en 3 X 2 = 5, dado que la expresión para la suma es el patrón correcto, 3 + 2 = 5, —tres y dos son cinco— y forma parte de nuestro repertorio memorístico, pero para nada nos resulta familiar la asociación 3, 2, 7 con cualquiera de las dos operaciones aritméticas.
Vemos estas interferencias de patrones en los procesos de aprendizaje de nuestros niños y jóvenes y aún en adultos instruidos. Entre los 6 y 7 años de edad, los niños aprenden de memoria muchas sumas con números de hasta dos dígitos, pero son típicos los errores en las sumas que coinciden con el inicio del aprendizaje de las tablas de multiplicar, 3 + 2 = 6 será recurrente si no se interviene eficazmente en su corrección (4).
Asimismo, las semejanzas de los patrones de pronunciación de los números interfiere con la rememoración de los productos correctos para 6 X 5 y 7 X 6, son respuestas típicas 6 X 5 = 35 y 7 X 6 = 36 porque riman con cinco y seis. Por el contrario, es muy raro observar que las personas cometan errores como 4 X 3 = 13 o 5 X 7 = 37 porque el 13 y el 37 no están en las tablas de multiplicar y nuestra memoria asociativa no los reconoce en el contexto de la multiplicación, pero el 35 y el 36 aparecen ambos en las tablas, por ello se activan y se interconectan simultáneamente en nuestros cerebros cuando queremos saber cuánto es 6 X 5.
Las peripecias para aprender matemáticas y, en especial, para dominar con maestría la aritmética, radican principalmente en la brillantez de nuestra inteligencia. W. W. Sawyer expone que los problemas en el aprendizaje de las tablas de sumar y multiplicar es al revés de cómo siempre se piensa y que la mayoría de nuestras dificultades con las matemáticas provienen del nivel de desarrollo de habilidades de nuestra la memoria asociativa y de la capacidad para reconocer patrones. En realidad es una paradoja, tenemos que aprender a discriminar muy finamente entre los casos muy parecidos para hallar, de manera correcta, los patrones de diferencias. En matemáticas buscamos patrones, establecemos modelos que hablan de regularidades y semejanzas, hacemos asociaciones y descubrimos relaciones entre los objetos, pero a la hora del cálculo exacto, estas virtudes nuestras pueden jugarnos malas pasadas (5), porque tendemos a generalizar semejanzas y atenuar disimilitudes.
A través de millones de años de evolución, nuestro cerebro fue equipado con habilidades para la supervivencia. Ser capaces de reconocer patrones es parte de esa herencia, así como visualizar relaciones y hacer juicios e inferencias rápidamente. Todos estos modos de pensamiento son esencialmente usados por nosotros sin rigor aparente, incluso están etiquetados peyorativamente como «pensamiento ligero».
Este «pensamiento ligero», muy útil para todos está descalificado socialmente, con mayor fuerza en el ámbito de las matemáticas, y es fuente de muchos prejuicios en esta materia de las resistencias para su aprendizaje.
Regresemos a nuestra evolución y al pensamiento ligero, sin la connotación peyorativa; por ligero, entendemos a la capacidad de nuestra inteligencia para hacer juicios y tomar decisiones rápidamente con relativamente poca información. Esta es una poderosa habilidad mental que supera por mucho nuestras capacidades de cálculo. Nuestros cerebros no evolucionaron para hacer cálculos complejos con números; no son adecuados (como las computadoras) para la operación precisa que exige la aritmética y, si a esto le aunamos el miedo que bloquea la inteligencia referido por Sheila Tobías y que bien explica Daniel Goleman, el problema se complica aún más (6).
Para el dominio de la aritmética necesitamos desarrollar los circuitos mentales —que fueron seleccionados durante nuestra evolución para tareas y por razones muy diferentes a las del cálculo— en un arreglo que ensamble, en un orden apropiado, las funciones necesarias para operar con números. Utilizar nuestro cerebro para hacer aritmética, sin el entrenamiento debido (adaptaciones), es como usar la uña dura de nuestro dedo pulgar para hacer las funciones de un desarmador, de seguro tardaremos más en lograr el resultado deseado y muchas veces la uña se romperá antes de alcanzar el éxito. No es posible pensar que podemos usar todas las partes de nuestro cuerpo, ni todas nuestras herramientas cognitivas como si fueran «multiusos»o «multipropósitos», es necesario reconocer que tenemos limitaciones.
Aprendemos las tablas de multiplicar utilizando nuestra habilidad para recordar patrones de sonidos —la audición es el primero de los sentidos de la percepción que se desarrollan durante la gestación(7)— y debido a los efectos de interferencia entre patrones muy parecidos, requerimos de un mayor esfuerzo para aprender las tablas. Lo mismo nos sucede cuando queremos distinguir a un par de gemelos idénticos, requerimos verlos juntos y entrenarnos en la percepción de finas diferencias entre ellos para discriminar eficazmente entre uno y otro.
Es un hecho conocido desde hace mucho tiempo que las personas que aprenden una segunda lengua siguen haciendo cálculos en su lengua materna, no importa qué tan fluidos sean en el otro idioma y aun cuando logren pensar en la segunda lengua, generalmente regresan a la primera para calcular y luego traducen el resultado, porque es más fácil usar los nombres de los números en la primera lengua que reaprender las tablas de multiplicar en otro idioma (8).
Siguiendo a Devlin en su análisis sobre la manera de contar en el idioma inglés, nosotros podemos notar, por analogía, que el nombrar los primeros números de un dígito, en español, no tiene dificultad, pero pasando del diez, en la estructura aritmética que usamos, cuenta la posición del dígito y el número 11 se escribe con dos unos que significan diez y uno, pero al nombrarlo no decimos “diez y uno”, esto es, el nombre del número en nada refleja la estructuración posicional del sistema numérico, porque el símbolo 11 se llama once. Igual sucede con el 12 (doce), 13 (trece), 14 (catorce) y 15 (quince); los números siguientes, 16 (dieciséis), 17 (diecisiete), etc, hasta el 19 (diecinueve) no tendrán problema, la estructura de nominación coincide con la numérica por posición. Pero el veinte no tiene siquiera una mínima relación parecida a la palabra dos en español; por ello, pasar del 19 al 20 y nombrar la palabra veinte les cuesta más trabajo a los niños. Hay que hacer muchas conexiones asociativas en la memoria o inventarlas por completo para que puedan vincular el símbolo 20 con su nombre y significado. Después de esto, 21 (veintiuno), 22 (veintidós), etc, no presentan mayor problema. El (30) treinta es menos difícil que el veinte porque empieza con la sílaba tre, igual que el tres, y de igual forma se siguen las próximas decenas 40 (cuarenta), 50 (cincuenta), etc. Las estructuras lingüísticas de nominación y las de composición numérica no se corresponden completamente, lo cual obliga a realizar un mayor esfuerzo en el aprendizaje de los nombres de los números y en la comprensión del sistema de numeración, tanto, que una vez superada esta primera etapa de conteo, los niños que continúan aprendiendo hasta el doscientos, dicen, al inicio de su aprendizaje, “ciento noventa y ocho, ciento noventa y nueve y ciento cien”, en lugar de doscientos. Según Devlin (9), a los chinos, japoneses, coreanos y tailandeses no les sucede esto, pues los nombres de los números son sencillos (de una sílaba) y la estructura lingüística para la nominación de los números, pasando el diez, es idéntica a la del sistema numérico, de tal suerte que los niños chinos aprenden más rápido a contar que los occidentales y por supuesto, las tablas de multiplicar son dominadas rápidamente y con mayor facilidad. Las diferencias en las habilidades numéricas de los niños chinos y los occidentales llegan a ser de hasta un año, esto es, para ponerlo en palabras de Devlin, mientras los niños occidentales de cuatro años cuentan hasta el 15 con trabajos, los infantes chinos ya se aprendieron hasta el 40, cosa que para nuestros pequeños representará un año más de esfuerzo (10).
Definitivamente, el poder trasladar o yuxtaponer una estructura lingüística a una aritmética sin tener que inventar o crear las reglas de relación (estructura de inferencia), facilita las cosas (11). En nuestro caso tenemos que elaborar arreglos en nuestras estructuras lingüísticas y en nuestra memoria asociativa para operar con las estructuras matemáticas, esto es, debemos crear los vínculos metafóricos y las metáforas que nos permitan apropiarnos de la multiplicación con habilidad para operar con ella.
Notas:
1. Utilizamos “subvocalizar” para sintetizar la acción mental de evocar el sonido de la palabra cuando se dice en voz alta.
2. Dehaene Stanislas, citado por Keith Devlin, The Math Gene, 2000. p. 68.
3. Stanislas Dehaene. The Number Sense, p. 127. Notas: (1) el autor no aclara que usa los nombres de las personas y el signo X (por) para asociarles sus direcciones, con lo cual hace una recodificación simbólica, convirtiendo las expresiones escritas en el lenguaje habitual en una metáfora aritmética. (2) Dejamos las expresiones principales en el idioma del autor para no modificar el ejemplo al traducirlo.
4. Estas observaciones son de nuestra experiencia adquirida con 120 niños en edades entre 6 y 8 años durante los años 1998-2001, en el Centro de Matemáticas Villa de Cortés.
5. W. W. Sawyer. 1982. Prelude to Mathematics. p. 31
6. Sheila Tobías. 1995. Overcoming Math Anxiety, p. 41. El miedo es una de las emociones primarias con las que nos equipó la biología y su función es obligarnos a tomar decisiones rápidas como huir, paralizarnos, etc, para sobrevivir ante una situación de peligro. Daniel Goleman, 1998. Inteligencia emocional. p. 23.
7. Sabbagh, K. y Barnard, C. 1984. El cuerpo viviente. Desarrollo inicial del feto. p. 188.
8. Devlin, K.. Op. Cit. p. 63.
9. Ibid. p. 65
10. Ibidem.
11. En otro artículo explicamos que en realidad
se construyen metáforas de un dominio del conocimiento a otro que además
involucran la elaboración de las metáforas de inferencia que permiten
la vinculación entre ellas.
Bibliografía.
Devlin, K. The Math Gene. How Mathematical Thinking Evolved
and Why Numbers Are Like Gossip. Basic Books, Great Britain, 2000.
Dehaene, S. The Number Sense. How the Mind Creates Mathematics. Oxford University
Press, N. Y. 1997.
Goleman, D. Educar con inteligencia emocional. Plaza & Janés. Barcelona.
1999.
Sabbagh, K. y Barnard, C. El cuerpo viviente. Plaza & Janes Editores. Barcelona.
1984.
Sawyer, W. W. Prelude To Mathematics. Dover Publications, Inc. New York, 1982.
Tobías, S. Over Coming Math Anxiety. Norton. E.U.A. y Cía. Nueva
York. 1995.